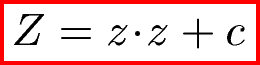Il
teorema di Pitagora nell'antichità
Si racconta, ma è leggenda, che
Pitagora abbia scoperto
il suo teorema mentre stava aspettando di essere ricevuto da
Policrate. Seduto in un grande salone del palazzo del
tiranno di Samo, Pitagora si mise ad osservare le piastrelle
quadrate del pavimento. Se avesse tagliato in due una
piastrella lungo una diagonale, avrebbe ottenuto due
triangoli rettangoli uguali. Inoltre l'area del quadrato
costruito sulla diagonale di uno dei due triangoli
rettangoli risultava il doppio dell'area di una piastrella.
Questo quadrato risultava infatti composto da quattro mezze
piastrelle, cioè da due piastrelle. Ma i quadrati costruiti
sugli altri lati del triangolo corrispondevano ognuno
all'area di una piastrella.
|
 |
|
Fig. 12 Dalle
piastrelle del pavimento al teorema di Pitagora. |
In altre parole il quadrato costruito
sull'ipotenusa è equivalente alla somma dei quadrati
costruiti sui due cateti. Questo risultava evidente nel caso
della piastrella quadrata, cioè di un triangolo rettangolo
isoscele: Ma poteva essere vero, si chiese Pitagora, anche
nel caso generale, con cateti di lunghezza diversa?
|
 |
|
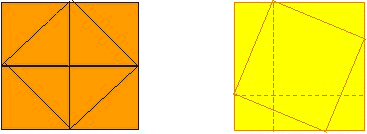
Fig. 13 Dai
triangoli rettangoli isosceli al caso generale. |
Studiando meglio la figura ottenuta
dall'osservazione delle piastrelle, Pitagora si accorse che
il quadrato formato da quattro piastrelle si poteva
scomporre in quattro triangoli rettangoli equivalenti e in
un quadrato il cui lato era uguale alla lunghezza
dell'ipotenusa di uno dei triangoli. Non fu quindi difficile
passare al caso generale di quattro triangoli rettangoli
qualsiasi, non più isosceli per i quali, come vedremo, vale
ancora il teorema.
|
 |
|
Fig.
14 Il
teorema di Pitagora. |
In realtà la storia del teorema è molto
più complessa e le sue origini, come abbiamo già detto,
risalgono almeno ad un migliaio di anni prima che Pitagora
si dedicasse allo studio dei triangoli rettangoli. Per
avviare la nostra indagine sul teorema partiamo dalla
formulazione che ne diede Euclide:
In
ogni triangolo rettangolo il quadrato del lato opposto
all'angolo retto è uguale ai quadrati dei lati che
contengono l'angolo retto.
Se lo riscriviamo in termini più moderni
abbiamo l'enunciato riportato generalmente nei testi
scolastici:
In ogni triangolo rettangolo il
quadrato dell'ipotenusa (oppure: l'area del quadrato
costruito sull'ipotenusa) è equivalente alla somma dei
quadrati dei due cateti (oppure: alla somma delle aree dei
quadrati costruiti sui due cateti).
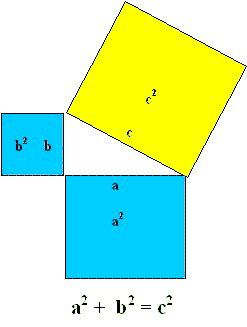
Se c indica la lunghezza
dell'ipotenusa e a e b quelle dei due cateti
possiamo scrivere il teorema in forma algebrica:
|
a2 +
b2 = c2 |
 |
Il teorema di Pitagora era noto un tempo
come "il ponte degli asini", il ponte che riusciva a
superare soltanto chi dimostrava di possedere sufficienti
attitudini per il pensiero astratto e per un metodo
deduttivo da applicare a procedimenti matematici quali erano
quelli proposti dai pitagorici.
|
 |
|
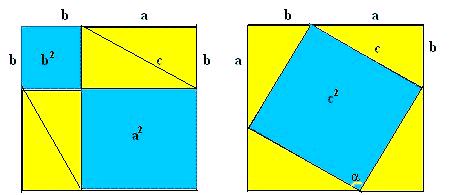
Fig. 15 Una
delle più semplici dimostrazioni di Pitagora,
fondata sulle equivalenze fra aree.
|
Ecco come Einstein ricorda il suo primo
incontro con il teorema:
Avevo 12 anni quando un mio vecchio zio mi enunciò il
teorema di Pitagora e dopo molti sforzi riuscii a
dimostrarlo. E’ stata un’esperienza meravigliosa scoprire
come l’uomo sia in grado di raggiungere un tale livello di
certezza e di chiarezza nel puro pensiero. E sono stati i
Greci per primi ad indicarcene la possibilità, con la
geometria.
Vediamo
una delle dimostrazioni più semplici, quella che
generalmente si trova sui testi scolastici e che riprende il
ragionamento che Pitagora potrebbe aver fatto osservando le
piastrelle quadrate nel palazzo di Policrate.
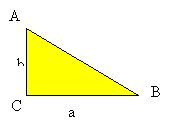
Dato il
triangolo rettangolo ABC (Fig. 16),
|
 |
|
Fig. 16 |
di cateti a, b e ipotenusa
c, costruiamo due quadrati equivalenti, che abbiano
come lato la somma dei due cateti, a + b (Fig.
15). Scomponiamo il primo di questi quadrati nei
due quadrati costruiti sui cateti e nei quattro triangoli di
figura, equivalenti al triangolo dato. Scomponiamo poi il
secondo quadrato nel quadrato costruito sull'ipotenusa e
negli stessi quattro triangoli. Se ai due quadrati grandi
togliamo i quattro triangoli equivalenti, otteniamo due
parti equivalenti: i quadrati costruiti sui cateti e il
quadrato costruito sull'ipotenusa.
|
 |
|
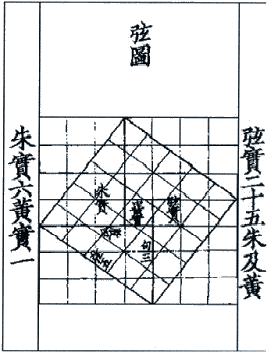
Fig. 17 Il
teorema kou ku o "di Pitagora" in
un'illustrazione originale del Chou Pei |
Attenzione però: la dimostrazione non è
ancora completa. E' necessario dimostrare ancora che le
parti più scure sono realmente i quadrati dei cateti e
dell'ipotenusa del triangolo dato. Per il primo quadrato a
sinistra (Fig. 15)
questo è evidente, dal modo in cui abbiamo eseguito la
scomposizione, cioè, come si dice, per costruzione.
Per il secondo quadrato a destra, sempre per costruzione,
possiamo dire che i suoi lati sono uguali all'ipotenusa del
triangolo. Resta da dimostrare che i suoi angoli sono retti.
Consideriamo l'angolo a, che sommato agli altri due
angoli aventi lo stesso vertice forma un angolo piatto. Ma
anche la somma degli angoli interni di un triangolo è uguale
a un angolo piatto, e quindi l'angolo a corrisponde
al terzo angolo del triangolo, che è retto. Allo stesso modo
si dimostra che anche gli altri angoli sono retti e quindi
che la figura è un quadrato.
Molte dimostrazioni si basano semplicemente sulla
scomposizione di aree in parti uguali. Una di queste
potrebbe provare che anche in Cina il teorema "di Pitagora"
era già noto almeno mille anni prima della nascita di
Pitagora. E' collegata a una figura, che si trova nel
Chou Pei Suan Ching (Fig. 17)
uno dei più antichi testi cinesi di matematica, Il libro
classico dello gnomone e delle orbite circolari del cielo,
scritto al tempo della dinastia Shang, 1500 - 1000 a. C..
Questa
figura potrebbe essere una dimostrazione del teorema di
Pitagora, chiamato dai cinesi kou ku. Nel disegno di
figura 17 si vede
infatti un triangolo rettangolo di lati 3, 4 e 5 e un
quadrato grande di lato 7 = 3 + 4.
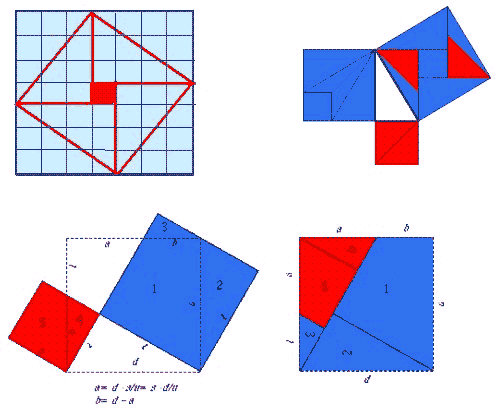
Lo schema della
figura 18 potrebbe aiutarci
a ricostruire la dimostrazione originale che purtroppo è
andata perduta. Come possibile percorso della dimostrazione
possiamo partire dai quattro triangoli rettangoli, di cateti
3 e 4, collocati attorno al quadrato centrale di lato 1.
|
 |
|
Fig. 18 Schema
del disegno del Chou Pei (in alto a sinistra) e
dimostrazioni del teorema di Pitagora di Liu Hui,
nella ricostruzione di D. B. Wagner, studioso danese
dell’Antica Cina (in alto a sinistra) e in quella di
Jöran Friberg, un matematico svedese (in basso). |
|
 |
|
Fig. 19 Liu
Hui, terzo secolo d.C.. |
Se raddoppiamo i quattro triangoli,
otteniamo il quadrato grande di lato 7. L'area di questo
quadrato grande è di 49 unità al quadrato. Per avere l'area
del quadrato piccolo e scuro, dobbiamo togliere l'area di
quattro triangoli, ognuno dei quali ha area 6 x 4, cioè 49 -
24 = 25. Il lato di questo quadrato misura quindi 5 unità ed
è l'ipotenusa del triangolo rettangolo di cateti 3 e 4.
Sempre in Cina Liu Hui, un grande matematico del terzo
secolo d. C., diede una dimostrazione del teorema "di
Pitagora" che è stata ricostruita da alcuni matematici
moderni seguendo le indicazioni che è stato possibile
ricuperare. Dice Liu Hui:
Siano il quadrato su kou [il
cateto a] rosso e il quadrato su ku [il cateto b]
blu. Usate il principio della mutua sottrazione e addizione
di specie simili per inserire i resti, in modo che non ci
sia alcun cambiamento nell'area con l'aspetto di un quadrato
sull'ipotenusa.
Le dimostrazioni riportate in
Fig. 18 sono graficamente
molto belle e non hanno bisogno di spiegazioni. Risultano
infatti evidenti le parti equivalenti in cui sono state
scomposte le figure.
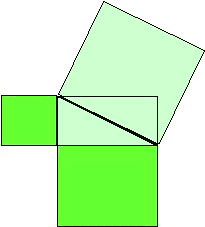
Anche dall'India arriva un enunciato del teorema di Pitagora
che ci autorizza a pensare come il teorema fosse già noto
agli indiani in epoche precedenti alla nascita di Pitagora.
Si legge infatti nei Sulbasutra, i testi che
contenevano le istruzioni per la costruzione degli altari,
riportati in forma scritta fra l'800 e il 600 a. C.:
La fune tesa per la
lunghezza della diagonale di un rettangolo forma un'area
pari alla somma di quella formata dal lato verticale e da
quello orizzontale.
|
 |
|
Fig. 20 Il
teorema di Pitagora secondo Sulbasutra. |
Si parla ancora di funi e di problemi
pratici. Ma la strada è aperta verso la matematica astratta.
Dall'Arabia (Fig.
21) arriva invece la dimostrazione di Thabit ibn
Qurra Marwan al'Harrani (826 - 901):
I triangoli ABC, CEH, CEM, BGD, EGL, AFL
sono tutti equivalenti. Inoltre osserviamo che il poligono
ABDEF può essere scomposto in due modi diversi:
|

|
|
e
|
|
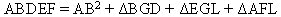
|
Dall'uguaglianza delle due relazioni e
dall'equivalenza dei triangoli indicati, ricaviamo:
|
 |
|
Fig. 21 La
dimostrazione araba di Thabit ibn Qurra |
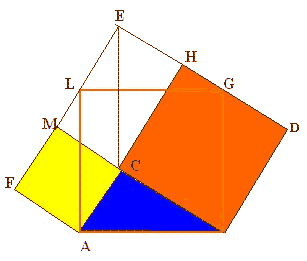
Pappo di Alessandria, nel quinto secolo
d. C. propose una costruzione che è una generalizzazione del
teorema di Pitagora, valida anche nel caso in cui il
triangolo non sia rettangolo.
|
 |
|
Fig. 22 La
dimostrazione di Pappo. |
Dato un triangolo qualsiasi ABC,
costruiamo sui suoi cateti i parallelogrammi BDEC e ACFG.
Inoltre prendiamo il segmento IL uguale a HC e costruiamo il
parallelogramma ABNM con i lati AM e BN paralleli e uguali a
IL. Poiché due parallelogrammi con la stessa base e la
stessa altezza sono equivalenti, abbiamo che BDEC è
equivalente a BPHC e che quest'ultimo è equivalente a BILN.
Quindi BDEC è equivalente a BILN. In modo analogo si
dimostra che ACFG è equivalente a AMLI. La somma di BDEC e
ACFG è dunque equivalente a AMNB.
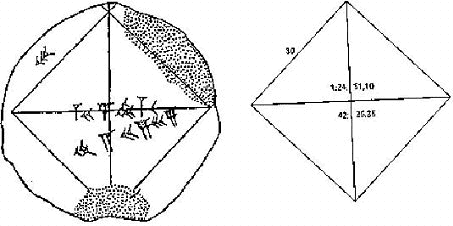
A questo punto possiamo rivedere, con
l'aiuto di uno schema (Fig. 23),
il collegamento tra il teorema di Pitagora e la famosa
tavoletta babilonese di cui parlavamo all'inizio del
capitolo.
|
 |
|
Fig. 23 Lo
schema della tavoletta babilonese, nella
ricostruzione di O. Neugebauer, con il calcolo della
diagonale di un quadrato di lato 30. A destra nel
sistema sessagesimale e a sinistra nel decimale. |
Il primo numero sulla diagonale è
1;24,51,10, dove il punto e virgola separa la parte intera
dalla parte decimale ed è in notazione sessagesimale. Lo
stesso numero nel sistema decimale è:
|
1 + 24/60 + 51/602 + 10/603
= 1,414213 ... |
che è un
valore approssimato della radice di 2.
Se il lato
del quadrato è 1, la diagonale è la radice quadrata di 1^2
più 1^2, cioè di 2. Se il lato è 30, sarà naturalmente il
prodotto di 30 per la radice quadrata di 2.
DE
Ma
la dimostrazione per eccellenza per i matematici è
sicuramente quella di Euclide,
riportata nel primo libro degli Elementi,
proposizione 47:
Nei triangoli retti il quadrato del
lato che sottende l'angolo retto è uguale alla somma dei
quadrati dei lati che contengono l'angolo retto.
Questa dimostrazione fa riferimento a
una figura (Fig. 24) che
è stata battezzata, per la sua forma particolare, mulino
a vento, coda di pavone o sedia della sposa.
Vediamola nei termini usuali per uno studente, come la
ritrova sul suo libro di geometria, nel capitolo dedicato ai
teoremi di Euclide.
|
 |
|
Fig. 24 La
sedia della sposa di Euclide. |
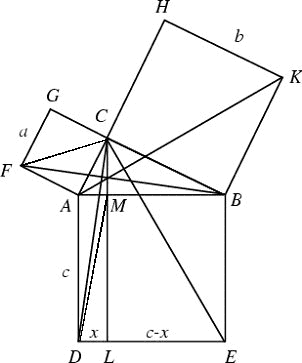
Dato il triangolo rettangolo ABC,
costruiamo i quadrati sui suoi lati e tracciamo CL parallelo
ad AD. I triangoli FAB e CAD sono uguali per il primo
criterio di uguaglianza. Hanno infatti AB = AD perché lati
dello stesso quadrato ABDE, inoltre AF = AC, perché lati
dello stesso quadrato ACGF e gli angoli FAB e CAD sono
uguali perché somma di un angolo retto e di un angolo in
comune, l'angolo CAB. Abbiamo perciò:
|
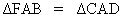 |
|
e |
|
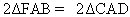 |
Inoltre i triangoli CAD e AMD hanno la
stessa base AD e la stessa altezza AM, e sono quindi
equivalenti:
D'altra parte i triangoli FAB e FAC
hanno anch'essi la stessa base AF e la stessa altezza AC,
quindi sono equivalenti:
Il rettangolo ADLM è perciò equivalente
al quadrato ACGF.
|
 |
|
Fig. 25 Euclide,
325-265 a.C. circa. Ritratto da A, Thevet, Vite di
uomini illustri, Parigi, 1584. |
Allo stesso modo dimostriamo che il
quadrato BKHC è equivalente al doppio del triangolo ABK e
quest'ultimo a sua volta è equivalente al doppio del
triangolo BCE, cioè al rettangolo BMLE:
Se sommiamo le due equivalenze
abbiamo:
Abbiamo così dimostrato che
La dimostrazione di Euclide, oltre a far
disperare ancora oggi tanti studenti, fece arrabbiare anche
il celebre filosofo Arthur Schopenahuer, il quale accusò il
grande matematico greco di aver costruito una figura che
porta a una interminabile catena di passaggi e che sembra
chiudersi su di noi come una “trappola per topi”.
Schopenahuer presentò anche una sua dimostrazione,
magnificandone, con la presunzione che lo
contraddistingueva, la chiarezza e la semplicità. In realtà
si tratta di una dimostrazione senza alcun valore,
riguardante soltanto il caso particolare del triangolo
rettangolo isoscele. Proprio quello che era stato il punto
di partenza per Pitagora, lo studio delle piastrelle del
palazzo di Policrate, ma soltanto un punto di partenza, per
arrivare alla dimostrazione generale del teorema.
|
 |
|
Fig. 26 Francobollo
greco dedicato al celebre teorema. |
| |
| |
|
per chi vuole approfondire |
|
TE |
| |
I teoremi
di Euclide
Il primo
teorema di Euclide:
| |
«In un triangolo
rettangolo il cateto è
medio proporzionale tra
la sua proiezione
sull'ipotenusa e
l'ipotenusa stessa»
|
| |
|
Lo
stesso teorema si può esprimere
geometricamente come segue:
| |
«In un triangolo
rettangolo il quadrato
costruito su un cateto è
equivalente al
rettangolo che ha per
dimensioni la sua
proiezione
sull'ipotenusa e
l'ipotenusa stessa»
|
| |
|
Il secondo
teorema di Euclide:
| |
«In un triangolo
rettangolo l'altezza
relativa all'ipotenusa è
media proporzionale tra
le proiezioni dei cateti
sull'ipotenusa»
|
| |
|
Il
secondo teorema può anche essere
espresso come:
| |
«In un triangolo
rettangolo il quadrato
costruito sull'altezza
relativa all'ipotenusa è
equivalente al
rettangolo che ha per
dimensioni le proiezioni
dei cateti
sull'ipotenusa»
|
 |
Gli
assiomi di Euclide
Tutta la geometria di Euclide
(qualche migliaio di teoremi) si
poggia su cinque postulati che il
matematico Playfair (1795) espose
nel seguente modo:
-
È sempre possibile tracciare una
retta tra due punti qualunque;
-
È sempre possibile prolungare
una linea retta;
-
È sempre possibile costruire una
circonferenza di centro e raggio
qualunque (ossia è sempre
possibile determinare una
distanza maggiore o minore);
-
Tutti gli angoli retti sono tra
loro congruenti;
-
Data una retta ed un punto
esterno ad essa esiste un'unica
retta parallela passante per
detto punto.
Il
quinto assioma è meglio conosciuto
come assioma di parallelismo
ed è quello che distingue la
geometria euclidea dalle altre.
In
funzione di come viene negato il
quinto postulato esistono due
diverse geometrie: quella
ellittica (non esistono rette
passanti per un punto esterno alla
retta data ad essa parallele) e
quella iperbolica (esistono
almeno due rette passanti per un
punto e parallele alla retta data).
|
|
per chi vuole approfondire |
|
FR |
| |
| |
|
Frattali |
| |
| |
|
Frattale di Mandelbrot
(Suggerita da Andrea Zanni)
|
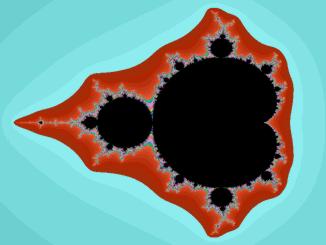 |
I
frattali sono fra tutti gli oggetti
matematici quelli che più impressionano
anche chi di matematica non capisce
assolutamente nulla. Si parte da una
figura come quella qui a fianco (che è
una rappresentazione dell'insieme di
Mandelbrot, il frattale forse più
famoso), e poi ci si abbandona
nell'osservare le linee e i colori, alla
ricerca di schemi che si ripetono
sempre, ma su scale diverse. L'occhio è
alla continua ricerca del confine della
figura, ma non lo può trovare, perchè
esso non esiste: se si ingrandisce
l'immagine si scoprono sempre nuove
insenature, sempre diverse ma sempre
simili a quella iniziale. E' questa
indefinitezza e autosomiglianza che
definisce concettualmente quello che è
un frattale. |
Ma cosa c'entra in
questo discorso la matematica? C'entra eccome,
perché i frattali sono degli oggetti matematici veri
e propri, definiti in una maniera rigorosa
attraverso delle formule. Lo studio della geometria
frattale è tutto sommato abbastanza recente, ed
inizia con Mandelbrot e Julia verso l'inizio del
ventesimo secolo. Solo la potenza di calcolo fornita
negli ultimi anni dall'avvento dei computer è però
riuscita a mostrarci in tutti i loro dettagli questi
straordinari oggetti. Le immagini che vediamo,
infatti, sono solo una rappresentazione degli
insiemi frattali, in cui ad ogni numero viene
associato un colore.
Ma il bello deve
ancora venire! Infatti nonostante si possa pensare
che un oggetto così complicato come un frattale
necessiti di una formula particolarmente lunga e
complessa per essere descritto, nulla è più lontano
dal vero. Che ci crediate o no, la formula con cui
viene generato l'insieme di Mandelbrot è la
seguente:
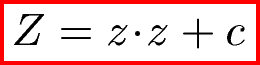
Si tratta
semplicemente di quella che in analisi matematica è
una parabola traslata rispetto all'origine di un
termine noto c! L'incognita è indicata con
z perché questa è la lettera che usualmente i
matematici usano per i numeri complessi. Il frattale
di Mandelbrot è infatti definito in un piano
semicomplesso (due assi sono per la parte reale ed
immaginaria dei numeri, e la rappresentazione
avviene grazie all'uso di colori diversi). Il modo
di procedere può essere molto brevemente descritto
nel modo seguente: per ogni punto X del piano
complesso, si pone c = X, e poi, a partire da
z = 0 + i*0, si calcola iterativamente Z
con la formula descritta sopra, fino a quando il suo
modulo sqr(Re[Z]^2 + Im[z]^2) diventa
maggiore di un certo valore G, che non è
altro che la grandezza del quadrato all'interno del
quale vogliamo rappresentare il frattale. Il numero
di volte che bisogna iterare il procedimento prima
di fermarsi è proprio il valore che associamo al
punto scelto X, che quindi coloriamo in base
ad una scala precedentemente definita (la
ripetizione infinite volte è un colore!). Seguendo
rigorosamente lo schema, grazie alla semplicissima
formula Z=z*z+c, si crea un oggetto
estremamente bello e complesso, che è proprio il
frattale di Mandelbrot.
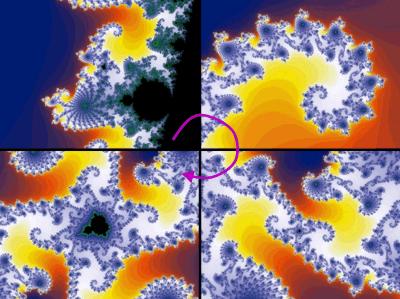
Giusto per
meravigliarsi ancora un po', qui sotto ci sono
quattro zoom progressivi di una zona chiamata "Sea
Horse" (Cavalluccio Marino), attraverso i quali
si possono intuire ancora una volta quelle che sono
le proprietà fondamentali dei frattali: l'autosomiglianza
su scale diverse, e l'indefinitezza del confine.
A titolo di
curiosità, infine, se si invertissero i ruoli di
z e c, ovvero fissato un generico c,
per ogni punto X scelto si ponesse z = X
e poi si iterasse il procedimento come sopra, si
otterrebbe un altro insieme frattale molto noto: il
frattale di Julia.
|
|
per chi vuole approfondire |
|